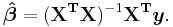Wiener filter
In signal processing, the Wiener filter is a filter proposed by Norbert Wiener during the 1940s and published in 1949.[1] Its purpose is to reduce the amount of noise present in a signal by comparison with an estimation of the desired noiseless signal. The discrete-time equivalent of Wiener's work was derived independently by Kolmogorov and published in 1941. Hence the theory is often called the Wiener-Kolmogorov filtering theory. The Wiener-Kolmogorov was the first statistically designed filter to be proposed and subsequently gave rise to many others including the famous Kalman filter. A Wiener filter is not an adaptive filter because the theory behind this filter assumes that the inputs are stationary.[2]
Contents |
Description
The goal of the Wiener filter is to filter out noise that has corrupted a signal. It is based on a statistical approach.
Typical filters are designed for a desired frequency response. However, the design of the Wiener filter takes a different approach. One is assumed to have knowledge of the spectral properties of the original signal and the noise, and one seeks the linear time-invariant filter whose output would come as close to the original signal as possible. Wiener filters are characterized by the following:[3]
- Assumption: signal and (additive) noise are stationary linear stochastic processes with known spectral characteristics or known autocorrelation and cross-correlation
- Requirement: the filter must be physically realizable/causal (this requirement can be dropped, resulting in a non-causal solution)
- Performance criterion: minimum mean-square error (MMSE)
This filter is frequently used in the process of deconvolution; for this application, see Wiener deconvolution.
Wiener filter problem setup
The input to the Wiener filter is assumed to be a signal, 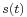 , corrupted by additive noise,
, corrupted by additive noise, 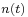 . The output,
. The output, 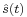 , is calculated by means of a filter,
, is calculated by means of a filter, 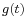 , using the following convolution:[3]
, using the following convolution:[3]
where
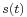 is the original signal (not exactly known; to be estimated)
is the original signal (not exactly known; to be estimated)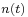 is the noise
is the noise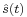 is the estimated signal (the intention is to equal
is the estimated signal (the intention is to equal 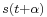 )
)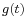 is the Wiener filter's impulse response
is the Wiener filter's impulse response
The error is defined as
where
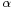 is the delay of the Wiener filter (since it is causal)
is the delay of the Wiener filter (since it is causal)
In other words, the error is the difference between the estimated signal and the true signal shifted by 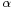 .
.
The squared error is
where
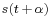 is the desired output of the filter
is the desired output of the filter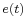 is the error
is the error
Depending on the value of 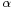 , the problem can be described as follows:
, the problem can be described as follows:
- If
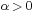 then the problem is that of prediction (error is reduced when
then the problem is that of prediction (error is reduced when 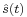 is similar to a later value of s)
is similar to a later value of s) - If
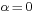 then the problem is that of filtering (error is reduced when
then the problem is that of filtering (error is reduced when 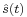 is similar to
is similar to 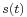 )
) - If
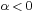 then the problem is that of smoothing (error is reduced when
then the problem is that of smoothing (error is reduced when 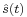 is similar to an earlier value of s)
is similar to an earlier value of s)
Writing 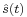 as a convolution integral:
as a convolution integral:
Taking the expected value of the squared error results in
where
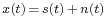 is the observed signal
is the observed signal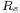 is the autocorrelation function of
is the autocorrelation function of 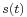
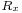 is the autocorrelation function of
is the autocorrelation function of 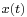
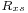 is the cross-correlation function of
is the cross-correlation function of 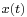 and
and 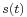
If the signal 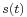 and the noise
and the noise 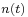 are uncorrelated (i.e., the cross-correlation
are uncorrelated (i.e., the cross-correlation 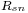 is zero), then this means that
is zero), then this means that
For many applications, the assumption of uncorrelated signal and noise is reasonable.
The goal is to minimize 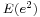 , the expected value of the squared error, by finding the optimal
, the expected value of the squared error, by finding the optimal 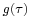 , the Wiener filter impulse response function. The minimum may be found by calculating the first order incremental change in the least square error resulting from an incremental change in g(.) for positive time. This is
, the Wiener filter impulse response function. The minimum may be found by calculating the first order incremental change in the least square error resulting from an incremental change in g(.) for positive time. This is
For a minimum, this must vanish identically for all 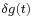 which leads to the Wiener-Hopf equation
which leads to the Wiener-Hopf equation
This is the fundamental equation of the Wiener theory. The right-hand side resembles a convolution but is only over the semi-infinite range. The equation can be solved by a special technique due to Wiener and Hopf.
Wiener filter solutions
The Wiener filter problem has solutions for three possible cases: one where a noncausal filter is acceptable (requiring an infinite amount of both past and future data), the case where a causal filter is desired (using an infinite amount of past data), and the finite impulse response (FIR) case where a finite amount of past data is used. The first case is simple to solve but is not suited for real-time applications. Wiener's main accomplishment was solving the case where the causality requirement is in effect, and in an appendix of Wiener's book Levinson gave the FIR solution.
Noncausal solution
Provided that 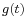 is optimal, then the minimum mean-square error equation reduces to
is optimal, then the minimum mean-square error equation reduces to
and the solution 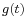 is the inverse two-sided Laplace transform of
is the inverse two-sided Laplace transform of 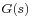 .
.
Causal solution
where
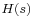 consists of the causal part of
consists of the causal part of 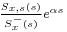 (that is, that part of this fraction having a positive time solution under the inverse Laplace transform)
(that is, that part of this fraction having a positive time solution under the inverse Laplace transform)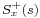 is the causal component of
is the causal component of 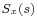 (i.e., the inverse Laplace transform of
(i.e., the inverse Laplace transform of 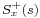 is non-zero only for
is non-zero only for 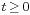 )
)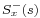 is the anti-causal component of
is the anti-causal component of 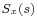 (i.e., the inverse Laplace transform of
(i.e., the inverse Laplace transform of 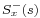 is non-zero only for
is non-zero only for 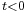 )
)
This general formula is complicated and deserves a more detailed explanation. To write down the solution 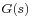 in a specific case, one should follow these steps:[4]
in a specific case, one should follow these steps:[4]
- Start with the spectrum
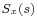 in rational form and factor it into causal and anti-causal components:
in rational form and factor it into causal and anti-causal components:
where 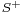 contains all the zeros and poles in the left hand plane (LHP) and
contains all the zeros and poles in the left hand plane (LHP) and 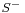 contains the zeroes and poles in the right hand plane (RHP). This is called the Wiener–Hopf factorization.
contains the zeroes and poles in the right hand plane (RHP). This is called the Wiener–Hopf factorization.
- Divide
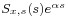 by
by 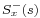 and write out the result as a partial fraction expansion.
and write out the result as a partial fraction expansion. - Select only those terms in this expansion having poles in the LHP. Call these terms
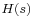 .
. - Divide
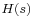 by
by 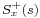 . The result is the desired filter transfer function
. The result is the desired filter transfer function 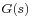 .
.
Finite Impulse Response Wiener filter for discrete series
The causal finite impulse response (FIR) Wiener filter, instead of using some given data matrix X and output vector Y, finds optimal tap weights by using the statistics of the input and output signals. It populates the input matrix X with estimates of the auto-correlation of the input signal (T) and populates the output vector Y with estimates of the cross-correlation between the output and input signals (V).
In order to derive the coefficients of the Wiener filter, consider the signal w[n] being fed to a Wiener filter of order N and with coefficients 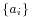 ,
, 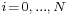 . The output of the filter is denoted x[n] which is given by the expression
. The output of the filter is denoted x[n] which is given by the expression
The residual error is denoted e[n] and is defined as e[n] = x[n] − s[n] (see the corresponding block diagram). The Wiener filter is designed so as to minimize the mean square error (MMSE criteria) which can be stated concisely as follows:
where 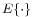 denotes the expectation operator. In the general case, the coefficients
denotes the expectation operator. In the general case, the coefficients 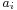 may be complex and may be derived for the case where w[n] and s[n] are complex as well. With a complex signal, the matrix to be solved is a Hermitian Toeplitz matrix, rather than Symmetric Toeplitz matrix. For simplicity, the following considers only the case where all these quantities are real. The mean square error (MSE) may be rewritten as:
may be complex and may be derived for the case where w[n] and s[n] are complex as well. With a complex signal, the matrix to be solved is a Hermitian Toeplitz matrix, rather than Symmetric Toeplitz matrix. For simplicity, the following considers only the case where all these quantities are real. The mean square error (MSE) may be rewritten as:
To find the vector ![\scriptstyle [a_0,\, \ldots,\, a_N]](/2012-wikipedia_en_all_nopic_01_2012/I/b8e665140939fe79c755981e702cea89.png) which minimizes the expression above, calculate its derivative with respect to
which minimizes the expression above, calculate its derivative with respect to 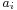
Assuming that w[n] and s[n] are each stationary and jointly stationary, the sequences ![\scriptstyle R_w[m]](/2012-wikipedia_en_all_nopic_01_2012/I/2b3536839f1cd1be41e01510c4d9203f.png) and
and ![\scriptstyle R_{ws}[m]](/2012-wikipedia_en_all_nopic_01_2012/I/82a399202dca62d29fa37b3e9d1b2226.png) known respectively as the autocorrelation of w[n] and the cross-correlation between w[n] and s[n] can be defined as follows:
known respectively as the autocorrelation of w[n] and the cross-correlation between w[n] and s[n] can be defined as follows:
The derivative of the MSE may therefore be rewritten as (notice that ![\scriptstyle R_{ws}[-i] \,=\, R_{sw}[i]](/2012-wikipedia_en_all_nopic_01_2012/I/ea5db4f02cdfd61b4034762aa3047cfb.png) )
)
Letting the derivative be equal to zero results in
which can be rewritten in matrix form
These equations are known as the Wiener-Hopf equations. The matrix T appearing in the equation is a symmetric Toeplitz matrix. These matrices are known to be positive definite and therefore non-singular yielding a unique solution to the determination of the Wiener filter coefficient vector, 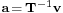 . Furthermore, there exists an efficient algorithm to solve such Wiener-Hopf equations known as the Levinson-Durbin algorithm so an explicit inversion of
. Furthermore, there exists an efficient algorithm to solve such Wiener-Hopf equations known as the Levinson-Durbin algorithm so an explicit inversion of 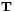 is not required.
is not required.
Relationship to the least mean squares filter
The realization of the causal Wiener filter looks a lot like the solution to the least squares estimate, except in the signal processing domain. The least squares solution, for input matrix 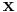 and output vector
and output vector 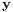 is
is
The FIR Wiener filter is related to the least mean squares filter, but minimizing its error criterion does not rely on cross-correlations or auto-correlations. Its solution converges to the Wiener filter solution.
See also
- Norbert Wiener
- Kalman filter
- Wiener deconvolution
- Eberhard Hopf
- Least mean squares filter
- Similarities between Wiener and LMS
- Linear prediction
References
- ^ Wiener, Norbert (1949). Extrapolation, Interpolation, and Smoothing of Stationary Time Series. New York: Wiley. ISBN 0-262-73005-7.
- ^ Standard Mathematical Tables and Formulae (30 ed.). CRC Press, Inc. 1996. pp. 660–661. ISBN 0-8493-2479-3.
- ^ a b Brown, Robert Grover; Hwang, Patrick Y.C. (1996). Introduction to Random Signals and Applied Kalman Filtering (3 ed.). New York: John Wiley & Sons. ISBN 0-471-12839-2.
- ^ Welch, Lloyd R. "Wiener-Hopf Theory". http://csi.usc.edu/PDF/wienerhopf.pdf.
- Thomas Kailath, Ali H. Sayed, and Babak Hassibi, Linear Estimation, Prentice-Hall, NJ, 2000, ISBN 978-0-13-022464-4.
- Wiener N: The interpolation, extrapolation and smoothing of stationary time series', Report of the Services 19, Research Project DIC-6037 MIT, February 1942
- Kolmogorov A.N: 'Stationary sequences in Hilbert space', (In Russian) Bull. Moscow Univ. 1941 vol.2 no.6 1-40. English translation in Kailath T. (ed.) Linear least squares estimation Dowden, Hutchinson & Ross 1977
External links
- Mathematica WienerFilter function
![\hat{s}(t) = g(t) * [s(t) %2B n(t)]](/2012-wikipedia_en_all_nopic_01_2012/I/0454aebc337dacdd0a8a9702a853f1f2.png)
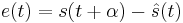
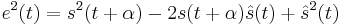
![\hat{s}(t) = \int\limits_{-\infty}^{\infty}{g(\tau)\left[s(t - \tau) %2B n(t - \tau)\right]\,d\tau}.](/2012-wikipedia_en_all_nopic_01_2012/I/e09708fc0d862dced1a0a3d91a77a683.png)
![E(e^2) = R_s(0) - 2\int\limits_{-\infty}^{\infty}{g(\tau)R_{xs}(\tau %2B \alpha)\,d\tau} %2B \iint\limits^{[\infty, \infty]}_{[-\infty, -\infty]}{g(\tau)g(\theta)R_x(\tau - \theta)\,d\tau\,d\theta}](/2012-wikipedia_en_all_nopic_01_2012/I/a7ed69adda04bd12f4bcda4dee94a4b4.png)
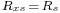
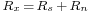
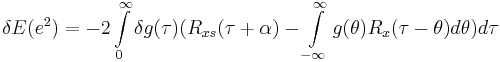
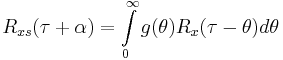
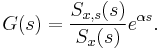
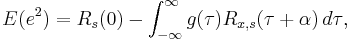
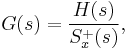
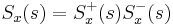
![x[n] = \sum_{i=0}^N a_i w[n-i] .](/2012-wikipedia_en_all_nopic_01_2012/I/25edcb637ab69b6f63cb08de9c326157.png)
![a_i = \arg \min ~E\{e^2[n]\} ,](/2012-wikipedia_en_all_nopic_01_2012/I/f67cd9bd8ba060e78e08c27d1786f725.png)
![\begin{array}{rcl}
E\{e^2[n]\} &=& E\{(x[n]-s[n])^2\}\\
&=& E\{x^2[n]\} %2B E\{s^2[n]\} - 2E\{x[n]s[n]\}\\
&=& E\{\big( \sum_{i=0}^N a_i w[n-i] \big)^2\} %2B E\{s^2[n]\} - 2E\{\sum_{i=0}^N a_i w[n-i]s[n]\} .
\end{array}](/2012-wikipedia_en_all_nopic_01_2012/I/4285107c56e77402580a6ba86a079e1c.png)
![\begin{array}{rcl}
\frac{\partial}{\partial a_i} E\{e^2[n]\} &=& 2E\{ \big( \sum_{j=0}^N a_j w[n-j] \big) w[n-i] \} - 2E\{s[n]w[n-i]\} \quad i=0,\, \ldots,\, N\\
&=& 2 \sum_{j=0}^N E\{w[n-j]w[n-i]\} a_j - 2E\{ w[n-i]s[n]\} .
\end{array}](/2012-wikipedia_en_all_nopic_01_2012/I/e299408f3386e553f792782cd68c0306.png)
![\begin{align}
R_w[m] =& E\{w[n]w[n%2Bm]\} \\
R_{ws}[m] =& E\{w[n]s[n%2Bm]\} .
\end{align}](/2012-wikipedia_en_all_nopic_01_2012/I/9d4a5870336bed73cc523fd73d5bbc37.png)
![\frac{\partial}{\partial a_i} E\{e^2[n]\} = 2 \sum_{j=0}^{N} R_w[j-i] a_j - 2 R_{sw}[i] \quad i = 0,\, \ldots,\, N .](/2012-wikipedia_en_all_nopic_01_2012/I/886f213bdf588b55ac2cc22ae3573ff9.png)
![\sum_{j=0}^N R_w[j-i] a_j = R_{sw}[i] \quad i = 0,\, \ldots,\, N ,](/2012-wikipedia_en_all_nopic_01_2012/I/75998b961d229d548270c1912477fdd3.png)
![\begin{align}
&\mathbf{T}\mathbf{a} = \mathbf{v}\\
\Rightarrow
&\begin{bmatrix}
R_w[0] & R_w[1] & \cdots & R_w[N] \\
R_w[1] & R_w[0] & \cdots & R_w[N-1] \\
\vdots & \vdots & \ddots & \vdots \\
R_w[N] & R_w[N-1] & \cdots & R_w[0]
\end{bmatrix}
\begin{bmatrix}
a_0 \\ a_1 \\ \vdots \\ a_N
\end{bmatrix}
=
\begin{bmatrix}
R_{sw}[0] \\R_{sw}[1] \\ \vdots \\ R_{sw}[N]
\end{bmatrix}
\end{align}](/2012-wikipedia_en_all_nopic_01_2012/I/44bc7cfdd49736f993a13547f6e2048e.png)